大型光学镜片的无应力夹持研究
为了尽量减小某系统中的大型反射镜因其自重造成的变形对光学系统精度的影响,应用有限元方法对该反射镜的两种定位支承方式的支承点位置进行仿真分析,从而得到在两种支承方式下减小反射镜工作区变形的最佳支承点位置。
1、前言
随着实际应用中的反射镜的不断大型化,其较大自重引起光学反射镜不同程度的变形,从而最终反映到光学系统的成像质量或光路引导精度上。为了减小镜片自重对光学系统精度的影响,提出了“无应力”夹持,由于既要夹持又要无应力是不可能的,确切地说“无应力”就是要获得一个合理的使镜片变形足够小的应力场,或者说是在镜片通光范围内(工作范围内)的应变均匀,或者衰减集中应力向镜片的传播。要实现“无应力”夹持,就必须知道支承点位置对于大型镜片的变形的影响。因此大型反射镜的支承环节不得不作为一个非常重要的技术环节加以考虑。本文主要讨论使反射镜在何种支承点位置下镜面变形最小。
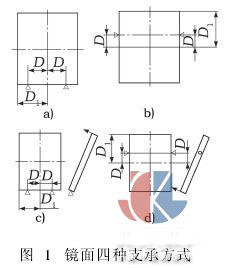
时至今日,人们已经对大型光学镜片的支承方式或理论作了大量的研究,并得出了大型光学镜片水平安装时支承点的规律,其支承点位于距镜片中心约为2/3倍边缘到中心的距离时,能获得镜片的最小变形量。但对于大型光学镜片与水平面成一定角度安装支承时的最佳支承点位置规律的研究甚少。为此,本文着重对与水平面成22. 5°和垂直安装的大型方形反射镜进行有限元仿真分析,确定此两种安装方式下底部两点支承和侧面两点悬挂支承时支承点的布置规律,如图1所示。图1a为底部两点支承方式,图1b为侧面两点悬挂支承方式,图1c为底部两点支承方式(上边缘线约束,方向如箭头所示),图1d为侧面两点悬挂支承方式(下边缘线约束,方向如箭头所示)。
2、构造有限元模型
有限元模型的建立是进行有限元分析的第一步,模型的好坏直接关系到计算结果的准确性,大型光学反射镜的有限元模型建立过程为:
1)模型支点位置的确定。本文根据方形反射镜(540mm*340mm*60mm)的两种安装方式,四种夹持方式分别建立有限元模型,并且底部支承方式支承点分别取D /D1=16/17(约为底部边缘处),D /D1=4/5处, D /D1=2/3处, D /D1=1/2处, D /D1= 1/4处;侧面夹持方式支承点位置分别取为中心支承(即D=0),D /D1= 1/5处,D /D1=2/3处,D /D1=7/9处,D /D1=25/27处,共10点进行分析比较。底部边缘到方形镜底部中心线距离D1=170mm,侧面边缘到侧面的中心线距离D1=270mm,由前面所选各点位置比例算出支承点的具体位置并分别建立有限元模型。
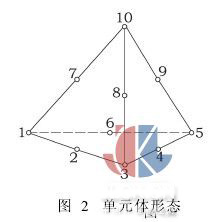
2)选择有限元单元。虽然反射镜物理模型不具有较复杂的几何形状,但在实际工程结构中应力场往往是随着坐标而急剧变化的,常应变单元体很难适应急剧变化的应力场,而采用高次位移函数不但可以得到高的计算精度,还能节约计算时间。为此建立满足此要求的10节点二次四面体单元,如图2所示,相应的形函数为:
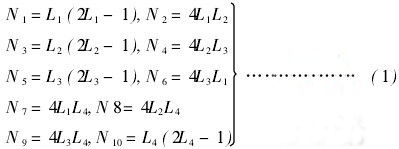
式中,Li为体积坐标; i=1,2,3,4。
所以单元位移用形函数表示为式(2):
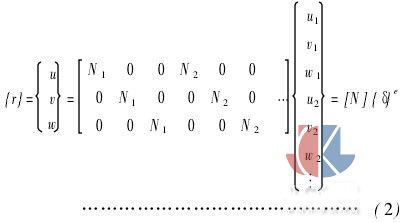
式中,r为单元位移;u为单元位移在X方向的分量; v为单元位移在Y方向的分量;w为单元位移在Z方向的分量;
![]()
为节点位移; i=1,2,3,…,10。
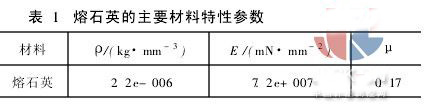
3)镜片材料的确定。镜片的材料选为熔石英,主要因为该材料具有优良的机械、物理性能和化学稳定性能,刚度大,材料比刚度(E /ρ)高,密度低,线膨胀系数较低,是机载光学系统、空间光学系统难得的优良光学材料。采用这种材料不仅可以有效减轻镜片的重量,而且可以减小加工或应用中镜面温度变化产生的变形,同时也可减小加工或装配中镜片的受力变形。熔石英的主要材料特性参数如表1所示。
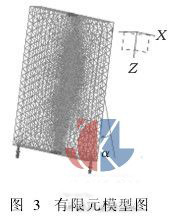
4)网格划分、边界条件和载荷的添加。应用大型有限元分析软件I2DEAS对镜体利用基于几何体的方式加入与夹持方式相应的边界条件和载荷,并采用自适应方法进行网格划分,将镜体离散为有限的单元和节点,最后生成的有限元模型一共有27248个单元,43220个节点。建立的有限元物理模型如图3所示。
3、有限元分析结果
经过一系列计算后得到关于不同安装方式在支承点处于不同位置时反射镜工作区的最大变形和最大应力与最小应力差的差值即应力差。应力差越大,应力均匀性就越差;反之越好。
镜片垂直和倾斜22.5°底部两点支承方式的计算结果见表2,侧面两点悬挂支承方式的工作区最大变形和应力差计算结果见表3。下面两表的应力单位为MPa,变形的单位为μm。
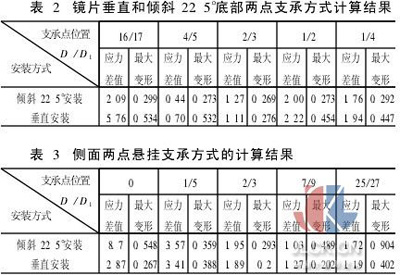
从表2、表3可以看出,无论是垂直安装,还是倾斜22.5°安装,底部支承时支承点布置在靠近边缘处即D /D1=16/17时有最大的变形量,22.5°安装和垂直安装时分别为0.299μm、0. 534μm,应力均匀性较差。随着D /D1的减小,反射镜的最大变形逐渐减小,应力的均匀性也有所提高,在D /D1=2/3时有最小的变形量0.269μm,应力均匀性较好。随着D /D1的进一步减小,反射镜变形又逐渐增大,应力均匀性也有所下降。垂直侧面支承时具有与底部支承时相同的规律,反射镜有较大的变形时的支承点位置同样靠近边缘处即D /D1=25/27和靠近中心线处即D=0,应力均匀性也较差,当支承点在D /D1=2/3时有最小的变形量,较好的应力均匀性。所以在上面列出的支承方式下,支承点的位置D应取为D≌2/3*D1。
4、结论
本文借助于有限元分析软件I2DEAS对大型反射镜在垂直和与水平面成22. 5°安装时单列支承点的最佳布置位置进行了研究,由分析计算结果得出了大型反射镜采用单列支承的支承点布置规律:将支承点布置在D≌2/3*D1处时,能获得镜面面形的最小变形,较好的应力均匀性。初步证明大型镜片无论是成何种角度安装,若采用此种支承方式,将支承点布置在D≈2/3×D1处时,可将镜面由于自重引起的变形对光学系统的影响最小化。
